F A C H H O C H S C H U L E W E D E L
Praktikum und Seminararbeit
im Wahlpflichtblock
Optik und Lasertechnik
Fachrichtung:
Physikalische Technik
Thema:
ATR - Spektroskopie
| Eingereicht von: |
Udo Becker |
Marco Schilling |
| Erarbeitet im: | 6. Semester |
|
| Abgegeben am: | 18. Januar 1996 |
|
| Referent: | Prof. Dr. Iven Pockrand |
|
ATR ("attenuated total reflection") bedeutet soviel wie verminderte oder geschwächte Totalreflektion, die bei Reflektion an absorbierenden Materialien auftreten kann. Die reflektierte Intensität wird gemessen und läßt Rückschlüsse über das absorbierende Medium zu. In der Industrie verwendet man solche Aufbauten um undurchsichtige Stoffe wie z.B. Lackschichten, Farben, Pasten und Polymerfolien mit einem IR-Spektroskop in einer ATR-Anordnung auszumessen.
Da die Schwächung der Intensität durch die geringe Eindringtiefe in das absor-bierende Medium 1 sehr gering ist, kommen häufig Aufbauten mit mehrfacher Reflexion zum Einsatz. Dieses Verfahren nennt sich dann FMIR ("frustrated multiple internal reflection")
Die Absorption in den oben genannten Materialien stellt eine Energieumwandlung dar. Es werden z.B. optische Phononen angeregt. Dies bedeutet makroskopisch: Es tritt eine Erwärmung des absorbierenden Mediums ein. Die Photonen der elektromagnetischen Strahlung können, je nach Wellenlänge, mit den Rumpfelektronen (UV>>VIS), den Valenzelektronen (UV/VIS) oder mit dem Gitter (IR) stoßen und dabei absorbiert werden. Dies ist gleichbedeutend mit einer Energieumwandlung bzw. mit dem auszumessenden Intensitätsverlust der reflektierten Strahlung.
Die mikroskopische Eigenschaft der Polarisation P des Materials wird durch die Dielektrische Funktion e bestimmt. Die makroskopischen Eigenschaften des Materials werden durch seine Brechzahl n bestimmt. e und n sind in der allgemeinen Form komplexe Größen. Die beiden Stoffeigenschaften hängen direkt voneinander ab und beschreiben das Verhalten von Stoffen was elektrische Felder (auch Wechselfelder) betrifft.
Bei unserem Versuchsaufbau wird ein anderer Effekt der ATR zur Bestimmung der Dielektrischen Funktion e von nahezu idealen Metallen ausgenutzt. Man stellt sich bei einem idealen Metall vor, daß die freien Elektronen im sogenannten Elektronengas vollständig delokalisiert sind. Eine Wechselwirkung mit den Atomrümpfen ist also nicht vorhanden. Diese freien Elektronen können nun (passender Wellenvektor und passende Frequenz vorausgesetzt) mit dem elektromagnetischen Wechselfeld der optischen Strahlung wechselwirken. Ein freies Elektronengas, auch Plasma genannt, besitzt eine Resonanzfrequenz ![]() , die sogenannte Plasmafrequenz. Wird mit entsprechender Frequenz und dem erforderlichen Wellenvektor k eingestrahlt, so wird das Plasma in Resonanzschwingungen gebracht.
, die sogenannte Plasmafrequenz. Wird mit entsprechender Frequenz und dem erforderlichen Wellenvektor k eingestrahlt, so wird das Plasma in Resonanzschwingungen gebracht.
Bei unserem Versuchsaufbau wird eine sogenannte Oberflächenplasmaschwingung angeregt. Unter welchen Bedingungen dies möglich ist soll nun im theoretischen Teil Abschnitt erörtert werden.
Im praktischen Teil sollen die Dipersionsrelation der Oberflächenplasmaschwingung und die Dielektrische Funktion für Silber und Chrom bestimmt werden.
Trifft ein Lichtbündel auf ein optisch dünneres Medium, so wird der Strahl beim Durchgang durch die Grenzfläche vom Lot weg gebrochen.
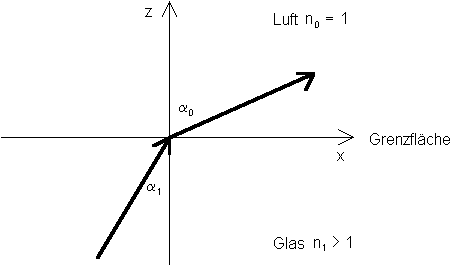
Abb 1: Reflektion am optisch dünneren Medium
Es gilt allgemein die Beziehung
(1) ![]()
Unter der Bedingung daß in diesem Falle n0 < n1 ist kann im sogennanten Grenzfall der Winkel ![]() = 90° erreicht werde. Ist dies der Fall, so ergibt sich der Sinus von
= 90° erreicht werde. Ist dies der Fall, so ergibt sich der Sinus von ![]() zu 1. (1) bestimmt nun, entsprechend umgeformt, die Bedingung für den sogenannten Grenzwinkel der Totalreflexion.
zu 1. (1) bestimmt nun, entsprechend umgeformt, die Bedingung für den sogenannten Grenzwinkel der Totalreflexion.
(2) ![]()
Im Winkelbereich ![]() wird alle einfallende Strahlung reflektiert.
Dies ist idealerweise so, wenn wir die Medien 0 und 1 als unendlich ausgedehnte
Halbräume annehmen und ein ideal kohärenter, d.h. unendlich ausgedehnter
monochromatischer Wellenzug die Grenzfläche passiert.
wird alle einfallende Strahlung reflektiert.
Dies ist idealerweise so, wenn wir die Medien 0 und 1 als unendlich ausgedehnte
Halbräume annehmen und ein ideal kohärenter, d.h. unendlich ausgedehnter
monochromatischer Wellenzug die Grenzfläche passiert.
Es ist nun aber Wellenmechanisch so, daß die gesamte Strahlung nicht direkt an der Oberfläche reflektiert wird. Wegen der Bedingung, das alles in der Natur stetig ist und der Betrachtung des Lichtes als Welle kann man vermuten und auch nachweisen, daß der elektrische Feldvektor E nicht abrupt an der Grenzfläche zu Null werden kann. Ein Teil der Strahlung muß in das Medium 1 übertreten und von dort aus wieder in das Medium 0 zurückgehen.
Eine entsprechende Darstellung ist in Abb. 2 wiedergegeben /1/.
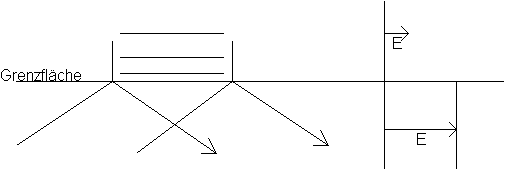
Abb. 2: Richtungsänderung vom k-Vektor an Grenzfläche
Die einfallende Strahlung wird an der Grenzfläche in das andere Medium übertreten und sofort wieder zurückgelenkt. Stellt man sich nun jeden einen einzelnen Strahl in einem Bogen zurückgeführt vor, so ergibt sich eine Strahlversatz von etwa einer Wellenlänge./1/
Eine andere Betrachtung geht von den Flächen maximaler Amplitude z.B. des E-Feldes aus. Aus den Stetigkeitsbedingungen :
(3) ![]()
folgt, daß die Welle im optisch dünneren Material parallel zur Grenzfläche verläuft. (Abb. 3)
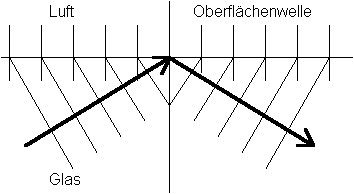
Abb. 3: Flächen konstanter Amplitude an Grenzfläche
Diese sogenannte Oberflächenwelle parallel zur Grenzschicht werden wir genauer betrachten. Zu den Eigenschaften einer solchen Oberflächenwelle ist nun folgendes festzuhalten /1/+/2/.
Diese Totalreflexion kann also nur stattfinden, wenn sich die Oberflächenwelle ungestört ausbreiten kann. Bringt man ein drittes Medium in die Nähe (<4l) der Grenzschicht, so wird die Totalreflexion gestört bzw. bei Abstand 0 unterbunden. Anhand dieser Störung lassen sich Aussagen über das Medium 1 machen.
Die sich bei der ungestörten Totalreflexion am optisch dünneren Medium ausbildende Oberflächenwelle sorgt dafür, daß alle eingestrahlte Energie die vom Medium 0 in das Medium 1 übertritt wieder reflektiert wird. Dies bedeutet, daß keinerlei Intensitätsverlust des reflektierten Strahls gegenüber dem einfallenden Strahl auftritt. Verwendet man als Medium 1 allerdings ein absorbierendes Material, so wird die Oberflächenwelle gedämpft bzw. deren Ausbildung ganz verhindert. Eine entsprechende Anordnung um solche Veränderungen auszumessen stellt das ATR dar.
2.3. Anregung einer OPS im Eingrenzflächensystem
Eine Einführung in die Theorie des benützten ATR-Aufbaus /3/ soll hier anhand eines Eingrenzflächensystems stattfinden. Wie sich im folgenden zeigen wird ist die Anregung einer Oberflächenplasmaschwingung mit einem solchen System nicht möglich. Es ist aber eine gute Möglichkeit um den Sachverhalt einfach darzustellen.
Das Eingrenzflächensystem soll aus einem Dielektrikum und einem Metall bestehen. Das Dielektrikum erhält den Index 0, das Metall den Index 1. In Abb. 4 ist der Aufbau einer solchen Schicht dargestellt.
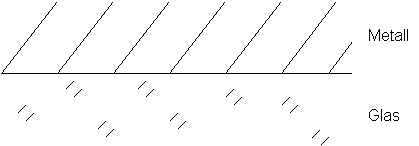
Abb. 4: Eingrenzflächensystem
Der theoretische Teil befaßt sich ausschließlich mit p-polarisiertem
monochromatischem Licht. P-Polarisation bedeutet hierbei, das der E-Feld-Vektor
parallel zur Einfallsebene (x-z-Ebene) schwingt. Auf diese Weise ist es möglich
die Amplitude des Vektors mit dem Winkel ![]() zu ändern. Es gelten bei dem gewählten Koordinatensystem folgende
grundlegende Eigenschaften der optischen Strahlung:
zu ändern. Es gelten bei dem gewählten Koordinatensystem folgende
grundlegende Eigenschaften der optischen Strahlung:
(5) ![]()
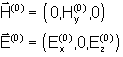
Mit Index 0 für Medium 0 und Indizes x, y, z für die entsprechenden Vektor-komponenten
Der magnetische Anteil läßt sich schreiben als:
(6) ![]()
mit ![]() = Maximalamplitude
= Maximalamplitude

Abb. 5: Eingrenzflächensystem k-Komponenten
In Abb. 5 sind die k-Vektoren in der x-z-Ebene dargestellt. Unten befindet sich wieder unser Medium 0 = Dielektrikum (z.B. Quarzglas), oben befindet sich unser Metall. Beiden Halbräumen sind die entsprechenden e zugeordnet. Für alle weiteren Betrachtungen ist nur die z-Abhängigkeit der Komponenten von Bedeutung. Es ergibt sich somit:
(7) 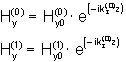
An der Grenzfläche (z=0) treffen zwei als unendlich ausgedehnt angenommene
Halbräume mit den Dielektrischen Funktionen ![]() und
und ![]() zusammen. In diesen Halbräumen
werden ebene Wellen mit den Wellenvektoren
zusammen. In diesen Halbräumen
werden ebene Wellen mit den Wellenvektoren ![]() und
und ![]() angenommen. Aus den Stetigkeitsbedingungen
der Grenzflächen ergibt sich nun:
angenommen. Aus den Stetigkeitsbedingungen
der Grenzflächen ergibt sich nun:
(8) 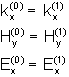
Es gilt folgende Dispersionsrelation für ebene Wellen im Dielektrikum:
(9) ![]()
im Medium (m).
Die Normalkomponenten lasses sich ausdrücken:
(10) ![]()
Wird nun ![]() , so muß die Normalkomponente
, so muß die Normalkomponente
![]() imaginär werden. Es handelt
sich dann um eine Oberflächenwelle. Wie vorher besprochen haben dann die
Felder der Oberflächenwelle ihr Maximum genau in der Grenzschicht (z=0).
Die Felder fallen zur positiven wie auch negativen z-Richtung hin exponentiell
ab.
imaginär werden. Es handelt
sich dann um eine Oberflächenwelle. Wie vorher besprochen haben dann die
Felder der Oberflächenwelle ihr Maximum genau in der Grenzschicht (z=0).
Die Felder fallen zur positiven wie auch negativen z-Richtung hin exponentiell
ab.
Da Medium 0 ein nur gering absorbierendes Material ist, erstreckt sich die Oberflächenwelle etwa 4 l in die negative z-Richtung. Dies ist nicht die Eindringtiefe, sondern der Bereich in welchem die Welle signifikant anwesend ist und gestört werden könnte. Das Metall hingegen verhindert mit seinen freien Elektronen ein tiefes Eindringen der Welle. Die Eindringtiefe beträgt etwa 10...15 nm /2/.
(11) ![]()
bei Metallen mit n// = Imaginärteil der Brechzahl.
Die Eindringtiefe ist definiert als der Abfall der Intensität auf 1/e.
Allgemein gilt /2/:
(12) ![]()
Es erfolgt hierbei keine Energieabstrahlung in die beiden Halbräume, man spricht von einer nichtstrahlenden Oberflächenplasmaschwingung.
Für die weiteren Betrachtungen ist noch zu erwähnen, daß die Dielektrische Funktion und die Brechzahl im allgemeinsten Falle komplexe Größen sind. Hierbei ist wichtig, daß der Real- als auch der Imaginärteil von physikalischer Bedeutung sind. Der Zusammenhang der beiden Größen besteht aus einer einfachen Gleichung
(13) ![]()
mit ![]() folgt
folgt
(14) ![]()
Handelt es sich um ein stark absorbierendes Medium (>10% Absorption), so sind die komplexen Ausdrücke zu verwenden. Bei uns ist dies mit einem Metall als Medium 1 gegeben.
Wir wollen nun eine Herleitung für die Dispersionsrelation unseres Eingrenz-flächensystems im folgenden darlegen /3/.
Aus (8) ergibt sich
(15) ![]()
Jetzt wird die Maxwellschen Gleichung
(16) ![]()
benötigt. Mit einsetzen von (7) folgt
(17) 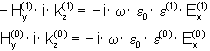
Mit (8) und (17) ergibt sich ein Gleichungssystem
(18) 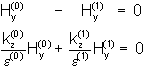
Durch z=0 und (7) folgt
(19) 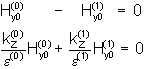
Nichttriviale Lösungen ergeben sich, wenn die Systemdeterminante D=0 ist.
(20) ![]()
Dies ist nun die Dispersionsrelation (w -k-Beziehung) einer Oberflächenwelle. Zur Diskussion bietet sich die folgende Schreibweise an, welche aus (20) und (10) entsteht
(21) ![]()
Es gilt weiter die Beziehung
(22) 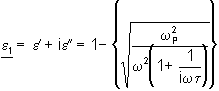
mit w P= Plasmafrequenz des Metalles; t = Relaxationszeit des Plasmas
für w
. t
>
>
1 läßt
sich ![]() in Real- und Imaginärteil
zerlegen. Es ergibt sich
in Real- und Imaginärteil
zerlegen. Es ergibt sich
(23) ![]() = Realteil und analog
= Realteil und analog
(24) ![]() = Imaginärteil.
= Imaginärteil.
Trägt man die Dispersionsrelation in einem Diagramm w über kx auf, so erhält man folgendes Bild (Abb.6)
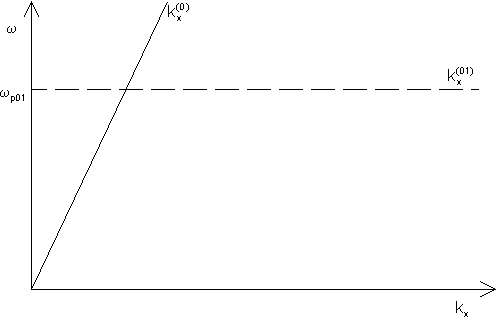
Abb. 6: Dispersionsrelation des Eingrenzflächensystems
Die Dispersionsrelation nähert sich für kleine kx asymptotisch der Lichtgeraden
(25) ![]()
im Dielektrikum 0 an und für große kx schmiegt sie sich
an die Asymptote ![]() an.
an.
(26) ![]()
mit Dielektrikum m und Medium 1 (Metall)
(27) ![]()
Man erkennt in Abb. 6, daß in diesem System keine Anregung der Oberflächen-plasmaschwingung
erfolgen kann, da für alle w gilt: ![]() .
Das Gleich-heitszeichen bezieht sich nur auf den Fall w
= 0.
.
Das Gleich-heitszeichen bezieht sich nur auf den Fall w
= 0.
2.4. Anregung einer OPS im Zweigrenzflächensystem
Die mathematischen Verhältnisse in einem Zweigrenzflächensystem sind sehr viel komplexer. Wir gehen deshalb nur im Ergebnis darauf ein. Für eine detaillierte Beschreibung verweisen wir auf /3/.
Zunächst eine Darstellung des Systems:
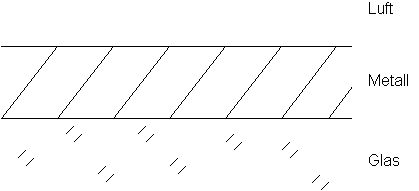
Abb. 7: Zweigrenzflächensystem
Man geht zunächst davon aus, daß es sich um zwei einzelne Eingrenz-flächensysteme handelt und trägt nun die erhaltenen 4 Dispersionsrelationen in einem gemeinsamen Diagramm auf.
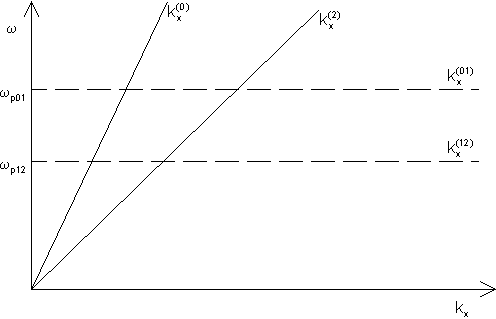
Abb. 8: Dipersionrelation eines Zweigrenzflächensystems
Die vier Dispersionsrelationen ergeben sich zu
(28) ![]() Lichtgerade
im Dielektrikum 0 (Luft)
Lichtgerade
im Dielektrikum 0 (Luft)
(29) ![]() Lichtgerade
im Dielektrikum 2 (Quarz)
Lichtgerade
im Dielektrikum 2 (Quarz)
mit ![]()
(30) ![]() Dispersionsrelation
OPS Grenfläche Metall-Luft
Dispersionsrelation
OPS Grenfläche Metall-Luft
(31) ![]() Dispersionsrelation
OPS Grenzfläche Metall-Quarz
Dispersionsrelation
OPS Grenzfläche Metall-Quarz
Man kann nun erkennen, das es Bereiche in Abb. 8 gibt, in denen der Vektor
![]() größer ist als der Vektor
größer ist als der Vektor
![]() der Oberflächenplasmaschwingung
an der Grenzfläche Metall 1 zu Dielektrikum 0.
der Oberflächenplasmaschwingung
an der Grenzfläche Metall 1 zu Dielektrikum 0.
In diesem Bereich können Oberflächenplasmaschwingungen angeregt werden,
wenn durch geeignete Maßnahmen der Vektor ![]() an einer Stelle w gleich dem Vektor
an einer Stelle w gleich dem Vektor ![]() wird. Eine solche Anpassung ist bei unserem Versuchsaufbau in Form der Änderung
von
wird. Eine solche Anpassung ist bei unserem Versuchsaufbau in Form der Änderung
von ![]() gegeben.
gegeben.
(32) ![]()
Es lassen sich so auf bequeme Weise die benötigten Wellenvektoren kx im Bereich der Totalreflexion
(33) ![]()
erzeugen.Die entsprechenden Wellenvektoren, welche so erzeugt werden können sind
(34) ![]()
Den Winkel ![]() kann man bei der Versuchsdurchführung
an dem Minimum der Reflektivität erkennen. Mit anderen Worten, die reflektierte
Intensität ist bei
kann man bei der Versuchsdurchführung
an dem Minimum der Reflektivität erkennen. Mit anderen Worten, die reflektierte
Intensität ist bei ![]() am geringsten,
da ein großer Teil der eingestrahlten Energie in der Metallschicht absorbiert
wird.
am geringsten,
da ein großer Teil der eingestrahlten Energie in der Metallschicht absorbiert
wird.
Bei all diesen Betrachtungen wurde ein ideales Metall vorausgesetzt, welches natürlich ideal an dem Dielektrikum 0 haftet und keinerlei Unebenheiten aufweist. Desweiteren wurden bestimmte Anforderungen an das reale Metall im zu messenden VIS-Bereich gestellt. Weitere Forderungen für das Zweigrenzflächensystem werden gemacht /3/ .
(35) ![]()
Dies bedeutet, das sich nur wenige Metalle (nahe Ideal wie z.B. Ag, Au) für diese Messmethode anbieten. Es wurde stillschweigend angenommen, das die beiden Grenzflächen "voneinander wissen". Da im Metall eine starke Dämpfung für optische Strahlung herrscht (vgl. (11) Eindringtiefe) sind nur Messungen an sehr dünnen Schichten möglich. Desweiteren existiert ein freies Elektronengas nur dann, wenn man einen fast idealen Kristall (Metall) benützt. Dies bedeutet: wenig Baufehler, große Korngröße, geringste Verunreinigungen usw.
Die Quintessez aus den Aufzeichnungen /3/ beinhaltet vier Terme, aus denen sich das kx zusammensetzt.
(36) ![]()
Hierbei bedeuten
![]()
![]() ist der Term, welcher die Resonanzlage
der Oberflächenplasma- schwingung beeinflußt.
ist der Term, welcher die Resonanzlage
der Oberflächenplasma- schwingung beeinflußt.
![]() ist ein Anteil, welcher nur
von der Dielektrischen Funktion des Metalls abhängt.
ist ein Anteil, welcher nur
von der Dielektrischen Funktion des Metalls abhängt.
![]() schließlich beschreibt
die sogenannte Strahlungsdämpfung der Oberflächen- plasmaschwingung
und ist u.a. von der Schichtdicke d des Metalls abhängig.
schließlich beschreibt
die sogenannte Strahlungsdämpfung der Oberflächen- plasmaschwingung
und ist u.a. von der Schichtdicke d des Metalls abhängig.
Als Strahlungsquelle wird eine Halogenglühlampe mit einem Hohlspiegel verwendet. Eine Kollimatorlinse parallelisiert den Strahl, der dann durch einen Strahlteiler geführt und mit einer Sammellinse auf ein Chopperrad abgebildet wird. Die gechoppte Stahlung ist notwendig, um die Daten über einem Lock-In-Verstäker auswerten zu können. Danach wird der Strahl wieder kollimiert und auf den Eintrittsspalt eines Prismenmonochromators abgebildet. Der jetzt monochromatische Strahl wird wieder kollimiert und durch einen Polarisator wird die benötigte p-polarisierte Strahlung erzeugt. Durch eine Blende wird der Strahldurchmesser begrenzt. Eine Zylinderlinse soll die brechende Wirkung des Quarzhalbzylinders, auf den die Metallschicht gebracht wird, kompensieren.
Der Quarzhalbzylinder ist im Zentrum eines Goniometertisches angebracht, auf dessen äußerem Ring sich ein Photomultiplier zur Detektion der reflektierten Strahlung befindet. Der Goniometertisch wird so angesteuert, daß sich der Photomultiplier um den doppelten Winkel des Quarzhalbzylinders bewegt. Somit ist realisiert, daß die reflektierte Stahlung immer die detektive Fläche des Photomultiplier trifft.
Die Ansteuerung des Goniometertisches und die Aufnahme der Meßwerte erfolgt
über einen Computer, der die Meßwerte von dem Lock-In-Verstärker
erhält. Die rechnergestützte Auswertung der erforderlichen Messungen
ist eine große Hilfe, da es anhand der Reflektivität, gemessen über
den Winkel ![]() , gilt, drei Parameter
zu bestimmen: Die Schichtdicke, den Realteil und den Imaginärteil der Dielektrischen
Funktion. Das Fitprogramm variiert diese drei Parameter so, daß eine angenäherte
Funktion zur tatsächlichen Messung einsteht. (Die Rechnung ist die Suche
nach der minimalen Abweichung zweier 3 dimemsionaler Raumflächen zueinander.)
, gilt, drei Parameter
zu bestimmen: Die Schichtdicke, den Realteil und den Imaginärteil der Dielektrischen
Funktion. Das Fitprogramm variiert diese drei Parameter so, daß eine angenäherte
Funktion zur tatsächlichen Messung einsteht. (Die Rechnung ist die Suche
nach der minimalen Abweichung zweier 3 dimemsionaler Raumflächen zueinander.)
Über den Strahteiler läßt sich der Strahl eines HeNe-Lasers in den Strahlengang einkoppeln, mit dem der Aufbau justiert und der Monochromator geeicht werden kann.
Die zu untersuchenden Schichten werden auf einen Substatträger aus Quarzglas mit einer Vakuumaufdampfanlage aufgedampft. Hierbei kann über die Frequenzänderung eines Schwingquarzes die aufzudampfende Schichtdicke eingestellt werde. Der Quarzglasträger wird dann mit einer Immersionsflüssigkeit mit dem Halbzylinder in optischen Kontakt gebracht. Die Brechzahl der Immersionsflüssigkeit entspricht der des Quarzglases, so daß keine Reflektionsverluste durch Brechzahlsprünge an den Übergängen auftreten. Die Substratträger haben eine definierte Dicke, die dem Quarzhalbzylinder entfernt wurde. Damit ist gewährleistet, daß sich die zu untersuchende Metallschicht immer in der Mitte des Goniometertisches befindet.
Es sollten von uns in den Messungen die Dispersionrelation (w-k-Beziehung) der OPS und die Abhängigkeit der Dielektrischen Funktion von der eingestrahlten Wellenlänge für Silber und Chrom aufgenommen werden.
Die für die Aufstellung der Dipersionsrelation benötigte Kreisfrequenz w ergibt sich aus der am Monochromator eingestellten Wellenlänge zu
(37) ![]() .
.
Für den Betrag des Wellenvektors in Luft folgt
(38) ![]() ,
,
ebenso können die Werte im Quarzglas sowie der OPS berecht werden.
(39) ![]()
(40) ![]()
mit ![]() =1,4588
=1,4588
Die dispersive Wirkung des Quarzglases ist hierbei vernachlässigbar.
|
l |
|
w |
|
|
|
|
[nm] |
[°] |
|
[ |
[ |
[ |
|
680 |
44,94 |
2,77 |
9,24 |
9,52 |
13,48 |
|
660 |
45,05 |
2,85 |
9,52 |
9,83 |
13,89 |
|
640 |
45,16 |
2,94 |
9,82 |
10,09 |
14,23 |
|
620 |
45,29 |
3,04 |
10,13 |
10,50 |
14,78 |
|
600 |
45,43 |
3,14 |
10,47 |
10,88 |
15,27 |
|
580 |
45,61 |
3,25 |
10,83 |
11,29 |
15,80 |
|
560 |
45,67 |
3,36 |
11,22 |
11,77 |
16,37 |
|
540 |
45,90 |
3,49 |
11,64 |
12,19 |
16,98 |
|
520 |
46,19 |
3,62 |
12,08 |
12,72 |
17,62 |
|
500 |
46,46 |
3,77 |
12,57 |
13,29 |
18,34 |
|
480 |
46,86 |
3,92 |
13,09 |
13,94 |
19,10 |
|
460 |
47,21 |
4,10 |
13,66 |
14,68 |
19,93 |
|
440 |
48,22 |
4,28 |
14,28 |
15,53 |
20,83 |
|
420 |
49,31 |
4,49 |
14,96 |
16,55 |
21,82 |
|
400 |
50,41 |
4,71 |
15,71 |
17,66 |
22,92 |
Tabelle 1: Dispersionsrelation für Silber
Die graphische Darstellung der Dispersionsrelation der Silberschicht ergibt den erwarteten Verlauf. Man sieht, daß die Dispersionsrelation der OPS für kleine Frequenzen gegen die Lichtgerade in Luft läuft. Für größere Frequenzen ist eine Krümmung erkennbar, der Schnittpunkt mit der Lichtgeraden im Quarzglas liegt jedoch im UV-Bereich und kann daher nicht bestimmt werden.
|
Kreisfrequenz [
Wellenvektor |
Abb. 9: Dispersionsrelation für Silberschicht
Die Messung der Dielektrischen Funktion für die Silberschicht ergab zufriedenstellende Ergebnisse über den gesamten visuellen Bereich. Die Literaturwerte nach /4/ sind als komplexe Brechzahl n gegeben, lassen sich also in die Werte der Dielektrischen Funktion mit (14) umrechnen.
|
l |
w |
e’ |
e’ |
e’’ |
e’’ |
|
[nm] |
|
gemessen |
Literatur |
gemessen |
Literatur |
|
700 |
2,69 |
-21,34 |
0,69 |
||
|
680 |
2,77 |
-19,43 |
0,37 |
||
|
660 |
2,85 |
-18,03 |
0,37 |
||
|
650 |
2,90 |
-17,15 |
0,59 |
||
|
640 |
2,94 |
-16,64 |
0,35 |
||
|
620 |
3,04 |
-15,42 |
0,35 |
||
|
600 |
3,14 |
-14,23 |
-13,70 |
0,34 |
0,45 |
|
580 |
3,25 |
-13,05 |
0,33 |
||
|
560 |
3,36 |
-12,42 |
0,28 |
||
|
550 |
3,42 |
-10,72 |
0,37 |
||
|
540 |
3,49 |
-11,25 |
0,25 |
||
|
520 |
3,62 |
-10,15 |
0,27 |
||
|
500 |
3,77 |
-9,26 |
-7,99 |
0,26 |
0,29 |
|
480 |
3,92 |
-8,25 |
0,25 |
||
|
460 |
4,10 |
-7,20 |
0,24 |
||
|
450 |
4,19 |
-5,55 |
0,27 |
||
|
440 |
4,28 |
-6,15 |
0,23 |
||
|
420 |
4,49 |
-5,17 |
0,21 |
||
|
400 |
4,71 |
-4,47 |
-3,72 |
0,22 |
0,29 |
Tabelle 2: Dielektrische Funktion für Silberschicht
In der graphischen Darstellung lassen sich die getroffenen Vorraussetzungen für die Dielektrische Funktion von Silber ablesen: Der Imaginärteil ist nahe Null, der Realteil ist negativ und vom Betrag wesentlich größer als der Imaginärteil. Der Verlauf der Kurven ist typisch für Metall: Zu größeren Wellenlängen werden die Beträge von Real- und Imaginärteil größer. Ebenso ist eine relativ gute Übereinstimmung mit den Literaturwerten gegeben.
Eine exakte Übereinstimmung mit Werten aus anderen Messungen bzw. Literatur war nicht zu erwarten, da die aufgedampften Schichten keinen definierten Aufbau haben. Wie in der Einleitung erwähnt wird diese Meßmethode u.a. benutzt, um Baufehler in Schichten zu erkennen. Man erhält also je nach Anordnung der Atome in der Schicht unterschiedliche Meßwerte. Eine exakte Übereinstimmung mit Meßwerten aus anderen Untersuchungen wäre daher nur mit einer ideal einkristallinen Struktur erreichbar.
|
e’,e’’
w
[ |
Abb. 10: Dielektrische Funktion für Silberschicht
Eine weitere Möglichkeit, die der ATR-Aufbau bietet, ist die Bestimmung der Schichtdicke dünner Schichten. Wie schon erwähnt wird durch das Fitprogramm neben der Dielektrischen Funktion die Schichtdicke als weiterer Parameter angepaßt.
Die für die Messungen benutzte Silberschicht hatte laut Schwingquarzanzeige der Vakuumaufdampfanlage eine Dicke von d = 51,0 nm. Dies ist für unseren Meßaufbau für Silber eine optimale Schichtdicke, um eine OPS anzuregen /3/. Betrachtet man die Meßwerte, so ist erkennber, daß über den gesamten Meßbereich zuverlässige Werte für die Schichtdicke geliefert werden.
|
l |
w |
d |
|
[nm] |
|
[nm] |
|
680 |
2,77 |
46,11 |
|
660 |
2,85 |
45,91 |
|
640 |
2,94 |
47,32 |
|
620 |
3,04 |
47,04 |
|
600 |
3,14 |
47,75 |
|
580 |
3,25 |
48,07 |
|
560 |
3,36 |
51,20 |
|
540 |
3,49 |
52,70 |
|
520 |
3,62 |
51,27 |
|
500 |
3,77 |
51,60 |
|
480 |
3,92 |
51,96 |
|
460 |
4,10 |
51,26 |
|
440 |
4,28 |
50,39 |
|
420 |
4,49 |
49,99 |
|
400 |
4,71 |
47,72 |
Tabelle 3: Schichtdicke der Silberschicht
Bei den Messungen an der Silberschicht können insgesamt befriedigende Ergebnisses geliefert werden werden. Es sollten auch Messungen an Chrom durchgeführt werden, die jedoch keine brauchbaren Ergebnisse brachten.
Die Messungen wurden an Schichten verschiedener Dicke durchgeführt. An einer sehr dünnen Schicht mit d = 19,4 nm (laut Schwingquarz) konnten mit einem IR-empfindlichen Photomultiplier drei Messungen mit relativ breiter Streuung der Werte aufgenommen werden.
|
l |
d |
e’ |
e’’ |
|
[nm] |
[nm] |
||
|
900 |
40,57 |
-16,20 |
17,54 |
|
850 |
23,53 |
-28,62 |
31,69 |
|
800 |
27,39 |
-21,09 |
26,69 |
Tabelle 4: Meßwerte für Chromschicht
An diesen drei Messungen läßt sich schon ablesen, daß die Bestimmung der Schichtdicke nicht sehr genau ist. Es wurden auch Messungen mit noch sehr viel stärker variierenden Werten durchgeführt, die hier nicht aufgeführt sind. Die große Varianz in den Werten der Dielektrischen Funktion weist ebenfalls auf unzuverlässige Zahlen hin. Leider konnten für den IR-Bereich keine Literaturwerte für Chrom gefunden werde.
Im sichtbaren Bereich gelang nur eine einzige Messung zufriedenstellend. Eine mit d = 30,4 nm bedampfte Chromschicht konnte bei l = 600 nm zu d = 42,9 nm vermessen werden. Die Dielektrische Funktion beträgt hier laut Messung e = -20,08 + i 24,52. Dieser Wert liegt nicht sehr weit vom Literaturwert bei l = 579 nm entfernt: e = -14,70 + i 28,81 /4/.
Arbeitet man mit Chrom, so muß bedacht werden, daß Chrom den Vorstellungen von einem idealen Metall längst nicht so nahe kommt wie beispielsweise Silber oder Gold. Die Vorstellung vom einem idealen Metall war aber in der theoretischen Betrachtung über die Anregung einer OPS vorrausgesetzt. Insbesondere das freie Elektronengas ist im Chrom nicht gegeben. Die Elektronen wechselwirken viel stärker mit den Rumpfatomen. Hierdurch läßt sich eine Oberflächenwelle schwerer anregen, das Minimun der Reflektivität wird verbreitert und abgeflacht. Eine weitere Vorraussetzung über die Größenordnung der Dielektrischen Funktion (35) wird von Chrom nicht erfüllt. Chrom wird deswegen allgemein auch kaum für reflektive Zwecke (z.B. Spiegel) genutzt.
13. August 2000, Udo Becker